Chung
Prenons \(\vec{U}\) et \(\vec{V}\) deux vecteurs de l'Espace. Notons P le plan contenant les vecteurs \(\vec{U}\) et \(\vec{V}\) et \(\theta\) l'angle entre ces deux vecteurs. \(\theta\) appartient au cadran 1.
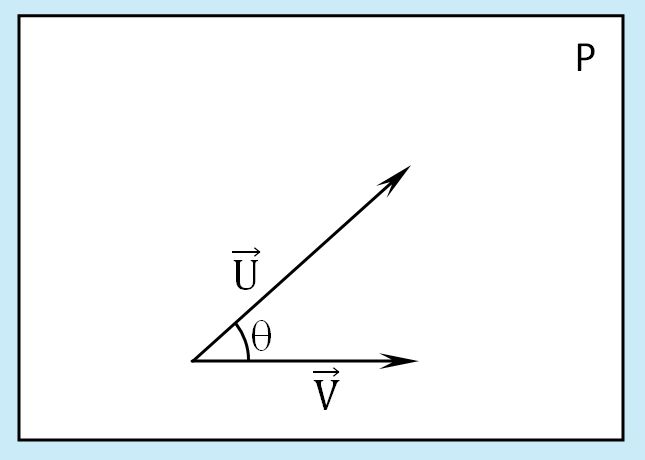
(1). \(\vec{U} \cdot \vec{V}\) est [[1]]
(2). \(\vec{U} \wedge \vec{V}\) est [[8]]
(3). \(\vec{U} \cdot \vec{V}\) est [[17]]
(4). \(\vec{U} \wedge \vec{V}\) [[15]]
Avec cette expression-ci :
z = \overbrace{ \underbrace{x}_\text{réel} + i \underbrace{y}_\text{imaginaire} }^\text{nombre complexe}
vous obtenez cela :
\( z = \overbrace{ \underbrace{x}_\text{réel} + i \underbrace{y}_\text{imaginaire} }^\text{nombre complexe} \)